A use case for dynamic randomization
This lesson provides a use case for configuring a dynamic randomization in Viedoc Designer, Viedoc Admin, and Viedoc Clinic. It also explains the algorithm that is used for assigning subjects to treatments, and how the calculations are executed.
| Important! The Randomization feature must be included in your study license in order for the randomization configuration to be available in production mode. You can still configure a randomization in demo mode without a license. |
Introduction
About the randomization service
Viedoc offers support for randomization. Subjects can be randomized using:
- static randomization: randomization based on a randomized list,
- dynamic randomization (Pocock and Simon): randomization based on an algorithm.
Dynamic randomization ensures a more even distribution of subjects across the treatment groups, with regard to prognostic factors that might influence the effect of treatment on the subjects.
The randomization in Viedoc is configured in a similar way for static and dynamic randomization. The main difference is that for static randomization, a list with outcomes (randomization numbers, treatment groups, and so on) - the randomization list - is created and uploaded by the user, while for dynamic randomization, an algorithm is used to assign subjects to a treatment group and the randomization list is created by the system.
It is possible to upload a separate allocation list that allocates an Investigational Product (IP) to the subject. When the subject is randomized, Viedoc informs the clinic user which IP should be given to the subject. The allocation list is most commonly used in double-blind studies. Uploading of the allocation list is done in a similar way for static and dynamic randomization.
Terminology
| Term | Definition |
|---|---|
| RTSM | Randomization and Trial Supply Management. |
| Blinded role | A role that does not know which treatment the subject is receiving. Most roles in a clinical trial should be blinded. |
| Unblinded Statistician |
A system role that can configure the randomization in Viedoc Admin. The Unblinded Statistician sees which subjects are assigned to which treatments, and should therefore not have any role in the study where he/she should not know this information. An Unblinded Statistician can never again work in a blinded role within that study. |
| Randomization list | A list for allocating subjects to treatments or groups. The randomization list shows all available slots in the randomization. When randomization has started (that is, when the first subject has been randomized), the randomization list also shows which subjects have been assigned to which treatment or group. |
| Allocation list | A list for allocating IP to subjects. The allocation list shows all available IPs. When randomization has started, the allocation list also shows which IPs have been assigned to which subjects. Advanced allocation can be set up and for this there are two options for the allocation list(s):
|
| Scope |
Defines the scope from which a randomization slot or an IP should be selected. One of the following scopes can be chosen:
|
| Factor (Prognostic factor) |
Items that might influence the effect of treatment on the subjects, and that are to be used as input when randomizing the subject. For example sex or age. Viedoc supports the use of drop-down lists, radio buttons, integer and free text data types as input items. |
| Outcome | Items to be populated by the randomization service, for example treatment group. |
| Blinded outcome | Items to be populated by the randomization service, that should remain blinded until after the subject has been unblinded or emergency unblinded for a specific subject. These items will not be visible for any user in the system, except for the Unblinded Statistician who can see them in Viedoc Admin, or until an emergency unblinding was performed (for details on how the emergency unblinding is performed in Viedoc Clinic, see Randomization, allocation and emergency unblinding). |
Workflow
Randomizations are configured in Viedoc Designer and Viedoc Admin, and executed in Viedoc Clinic. The schematic below depicts what different steps need to be taken, and which roles have permission to perform these steps, depending on the allocation configuration type as described below:
- Randomization, optionally together with allocation performed at the same time as the randomization within the same form. In this case the form is locked (and therefore not possible to be edited) after the randomization is performed in Viedoc Clinic.
The configuration workflow in this case looks as illustrated in the following image:

- Randomization, optionally together with advanced allocation allows you to set up the allocation in a more flexible way, including:
- Configuring individual forms for randomization and allocation, to keep the two steps separated in the study workflow
- The possibility to perform multiple allocations at different visits during the study
- The possibility to replace an already performed allocation with a new allocation
- The possibility to undo an already performed allocation
The configuration workflow in this case looks as illustrated in the following image:

This is a single-sourced file that should have the following content:
Introduction to randomization
Detailed instructions regarding these steps are described in:
- Setting up the randomization in Viedoc Designer
- Configuring a static randomizations in Viedoc Admin
- Configuring a dynamic randomization in Viedoc Admin
For a video tutorial on how to configure a static list randomization and a dynamic randomization, see:
Description of the use case
Let's consider the following scenario: We conduct a trial in which we compare three treatments: A, B and C. We want to randomly assign patients to these treatments, and we want treatment A to be allocated 50% of the time, and treatments B and C 25% of the time respectively. The prognostic factors that might influence the effect of the treatment on the subject, and that we would like to balance for in the randomization, are the subject's sex (male or female) and the subject's age (<= 30 or > 30). We consider it more important to balance for the subject's sex than for the subject's age, so we set a higher factor weight on the factor sex.
In summary:
- Three treatment groups: A, B and C.
- Allocation ratio for A:B:C = 2:1:1
- Two factors: sex (male or female) and age (<= 30 or > 30)
- Factor weights: 2 for sex, 1 for age.
The procedure
Actions to be performed in Viedoc Designer
Set up forms in Viedoc Designer
In this randomization example, we use two forms:
- Add Subject form - containing two items:
- Gender
- Age
- Treatment form (the randomization form) - containing three items:
- Gender - returns the value for Gender in the Add Subject form.
- Age - returns the value for Age in the Add Subject form.
- Treatment - containing a code list with three choices: A, B, and C. This item will be populated by the randomization service.
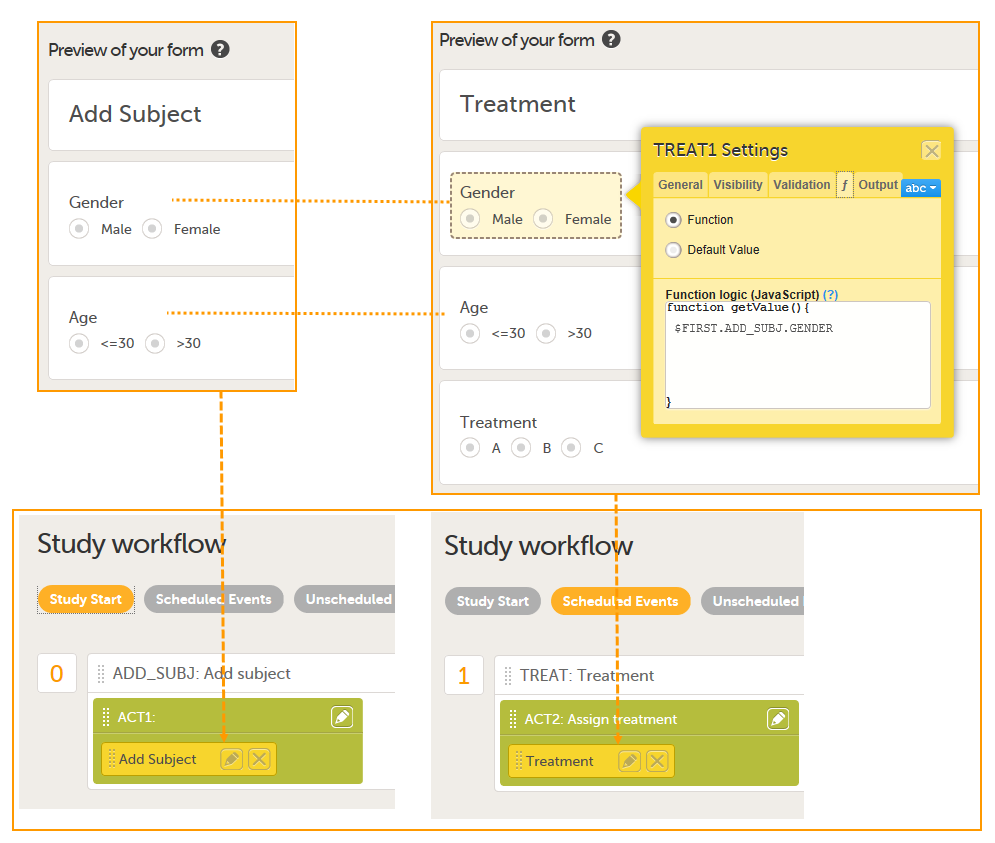 The form Add Subject is added to the activity ACT1 in the Add_SUBJ Study Start event. The form Treatment is added to the activity ACT2: Assign treatment in the Treatment event, which is the first scheduled event.
The form Add Subject is added to the activity ACT1 in the Add_SUBJ Study Start event. The form Treatment is added to the activity ACT2: Assign treatment in the Treatment event, which is the first scheduled event.
Note! The randomization form (here called Treatment) must contain all of the input factors and outcomes you intend to use for making assignments.
Tip! Once saved in Viedoc Clinic, the randomization form cannot be edited anymore. Add a message to the form asking the clinic user to make sure that the data are correct before randomizing the patient (see image below).
Tip! Because the Treatment item in the Treatment form is the item that will be populated by the randomization service, and should not be filled in by the clinic user, it may be a good idea to make it invisible to the clinic user as long as the patient is not randomized. In order to achieve this, you can set the visibility conditions On advanced conditions evaluates true for this item to TREAT!=null (show item when it is not null). Then, the clinic user cannot see the item when opening the form. But once the clinic user clicks Randomize, the randomization service allocates the subject to a treatment, the item is not equal to null anymore and appears in the form.
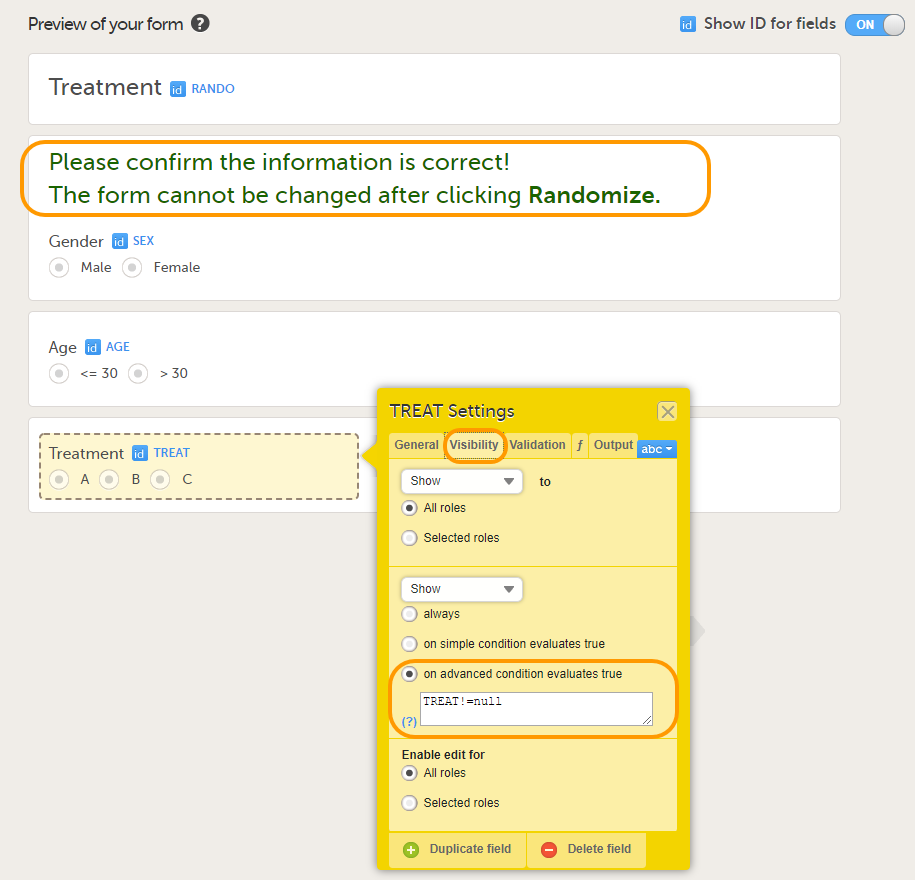
In this example, the randomization outcome (treatment) is not blinded. If you decide to set up a blinded outcome, this item has to be included in the randomization form as well. The blinded outcome will never be shown to the clinic user, it is not available in the export, and you cannot program visibility conditions or edit checks based on the blinded outcome.
Setting up the randomization in Viedoc Designer
The randomization mapping is set up under Study Settings in the study design in Viedoc Designer. The randomization mapping tells Viedoc where the randomization form is and how to use the variables on that form.
We set up the randomization as follows:
- We select the Event, Activity and Form for our Treatment form.
- As Factors, we select the Gender and Age items in the Treatment form.
- As Outcome, we select the Treatment item in the Treatment form. This item is going to be populated by the randomization service.
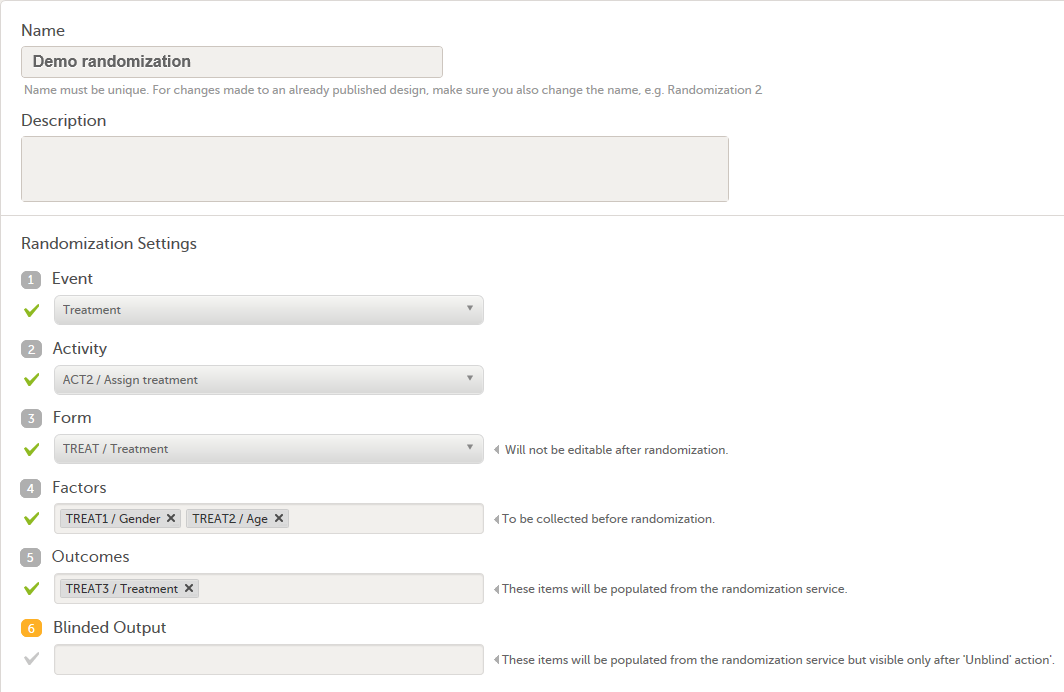
For step by step instructions on how to set up the randomization mapping in Viedoc Designer, see Setting up the randomization.
After the randomization mapping has been set up, the study design needs to be published for the randomization to become active.
Actions to be performed in Viedoc Admin
Inviting a user to the role Unblinded Statistician
The Study Manager needs to invite a user to the role Unblinded Statistician. The role Unblinded Statistician should only be given to users that are supposed to be unblinded and that do not participate in study evaluation procedures, otherwise the blind will break. An Unblinded Statistician can never work in a blinded role within that study.
For step by step instructions on how to assign roles to users, see Managing users (STM and SIM).
Configuring the dynamic randomization in Viedoc Admin
Note! The randomization can only be configured by users that are assigned the system role Unblinded Statistician.
To enter the Randomizations page, select the toolbox icon in the Randomization is on field in Viedoc Admin.
In this example, we do not use allocation, so we only set up a Randomization list, as follows:
- We set the Scope of the Randomization list to Study.
- As Factors, we select Gender and Age.
- As Outcome, we select Treatment
From the Randomization method dropdown list, we select Dynamic (Pocock/Simon).
Note! The dynamic randomization method can only be chosen if the following criteria are met:
- Only one outcome is selected
- The selected input factors, as well as the outcome, have a code list (no free text fields can be used).
Note! You will need to create the dynamic randomization configuration individually for demo mode and production mode after creating the dynamic randomization settings.
Select Approve settings & generate list. The Create configuration link is displayed:
 Select Create configuration to configure the dynamic randomization.
Select Create configuration to configure the dynamic randomization.
We configure the dynamic randomization as follows:
- As Variation method, we select Range (this is the difference between the highest and the lowest value in the set).
- We set the Probability to 800 (the equivalent of 80%).
- In our example, it is more important to achieve balance in the factor Gender than in the factor Age, so we set the Factor weights to 2 for Gender and 1 for Age.
- Because we want treatment A to be allocated 50% of the time, and treatments B and C 25% of the time respectively, we set the Allocation ratio to 2 for treatment A, and to 1 for treatment B and C.
- As Max slots (per list) we enter a maximum of 50 slots.
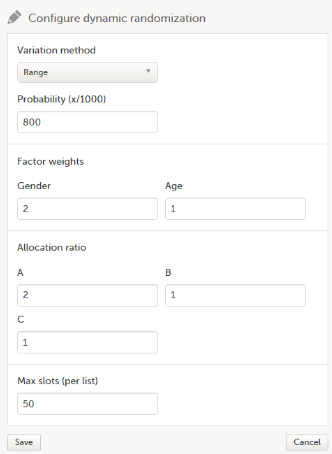
For step by step instructions on how to set up the randomization in Viedoc Admin, see Configuring a dynamic randomization.
Actions to be performed in Viedoc Clinic
Randomize a patient in Viedoc Clinic
When the clinic user has added a subject in Viedoc Clinic (i.e., filled in the Add Subject form), and opens the Treatment form, the values for Gender and Age are automatically populated from the Add subject form. Upon clicking Randomize, the subject will be assigned to one of the treatment groups. The Treatment item will appear in the form, populated by the randomization service.
 Note! Upon randomizing the subject, the randomization form (Treatment form) becomes read-only. This means that no item in the Treatment form will be editable, not even if the value for Gender or Age changes in the original Add subject form.
Note! Upon randomizing the subject, the randomization form (Treatment form) becomes read-only. This means that no item in the Treatment form will be editable, not even if the value for Gender or Age changes in the original Add subject form.
Calculations behind the scenes
This section explains how the calculations are made for assigning one of the three treatments (A, B or C) each time a new subject is randomized.
References
The underlying theory for the dynamic randomization method that is implemented in Viedoc is described in the following articles:
- Pocock S.J. and Simon R. Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trial. Biometrics 1975;31:103-115.
- Miller E. Probability sharing in a modified Pocock-Simon method. 12th Int. Conf. of S.C.M.A Jun 22, 2005.
The Donald E. Knuth's subtractive random number generator algorithm that is used in the modified Pocock and Simon method implemented in Viedoc is described in the following article:
- Donald. E. Knuth. The Art of Computer Programming, volume 2: Seminumerical Algorithms. Addison-Wesley, Reading, MA, second edition, 1981.
Concepts and terminology for dynamic randomization
The following table lists the terms that the algorithm used for dynamic randomization according to the Pocock and Simon method is based on.
| Term | Description | Calculated as |
|---|---|---|
| D | The amount of variation in the set of values for a factor |
|
| G | The total amount of imbalance across all factors | Sum of weighted D (D multiplied by factor weight) for all factors. |
| P (p) | The probability with which the treatment that minimizes imbalance is assigned |
The probability determines the extent to which one wishes to favour the treatment group that would lead to the smallest imbalance. During the randomization, the probability P for each treatment assignment is calculated, based on a probability cut-off. This probability cut-off (referred to as p below) is a static decimal between 0 and 1 that is provided by a statistician. In Viedoc, the probability cut-off has to be entered as x/1000. So for a p of 0.8 (80%), the number 800 should be entered. During randomization, P for each treatment will be distributed as follows:
|
| Random | A random number between 0 and 1 | Generated using Donald E. Knuth's subtractive random number generator algorithm |
| seed | A value used to initialize the random number generator | Based on the number of ticks to represent the current date |
Procedure
Using the above algorithms, a frequency table is calculated for each new subject to be randomized. A random number greater than or equal to 0 and less than 1 is generated using a seed value based on the number of ticks to represent the current date. Using the Ps and this random number, a treatment index is chosen and the patient is thereby assigned this treatment.
When a new subject is added and should be randomly assigned a treatment, the following calculations are performed:
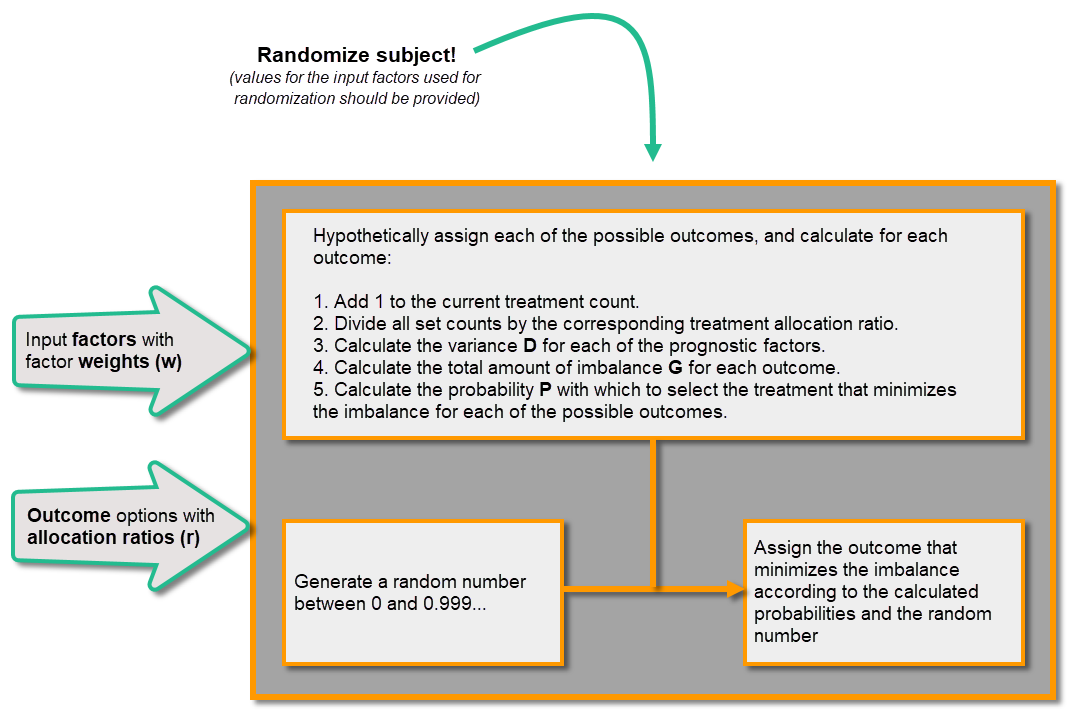
Calculations
Once the first subject is randomized, it is possible to download the randomization list from Viedoc Admin.
 An Excel file is downloaded, which has the following three sheets:
An Excel file is downloaded, which has the following three sheets:
- Configuration (1) - a summary of the factors and outcomes and their code lists, and the randomization details (randomization method, variation method, probability, maximum number of slots per list, factor weights and allocation ratio).
- Current distribution (2) - a summary of the number of entries sorted by the factors and the outcome. In our example, we can see how many subjects are assigned to each treatment, how many of them are males/females and how many are aged <=30 and >30.
- Slots (3) - one row for each randomized subject, listing:
- the details of the randomization: factors and outcomes, subject details, user details (e-mail address) of the clinic user who randomized the subject, and date and time of randomization,
- the details of the applied algorithm: variation method, probability P, factor weights, allocation ratio, maximum number of slots per list, Gs, Ps, Random and Seed.
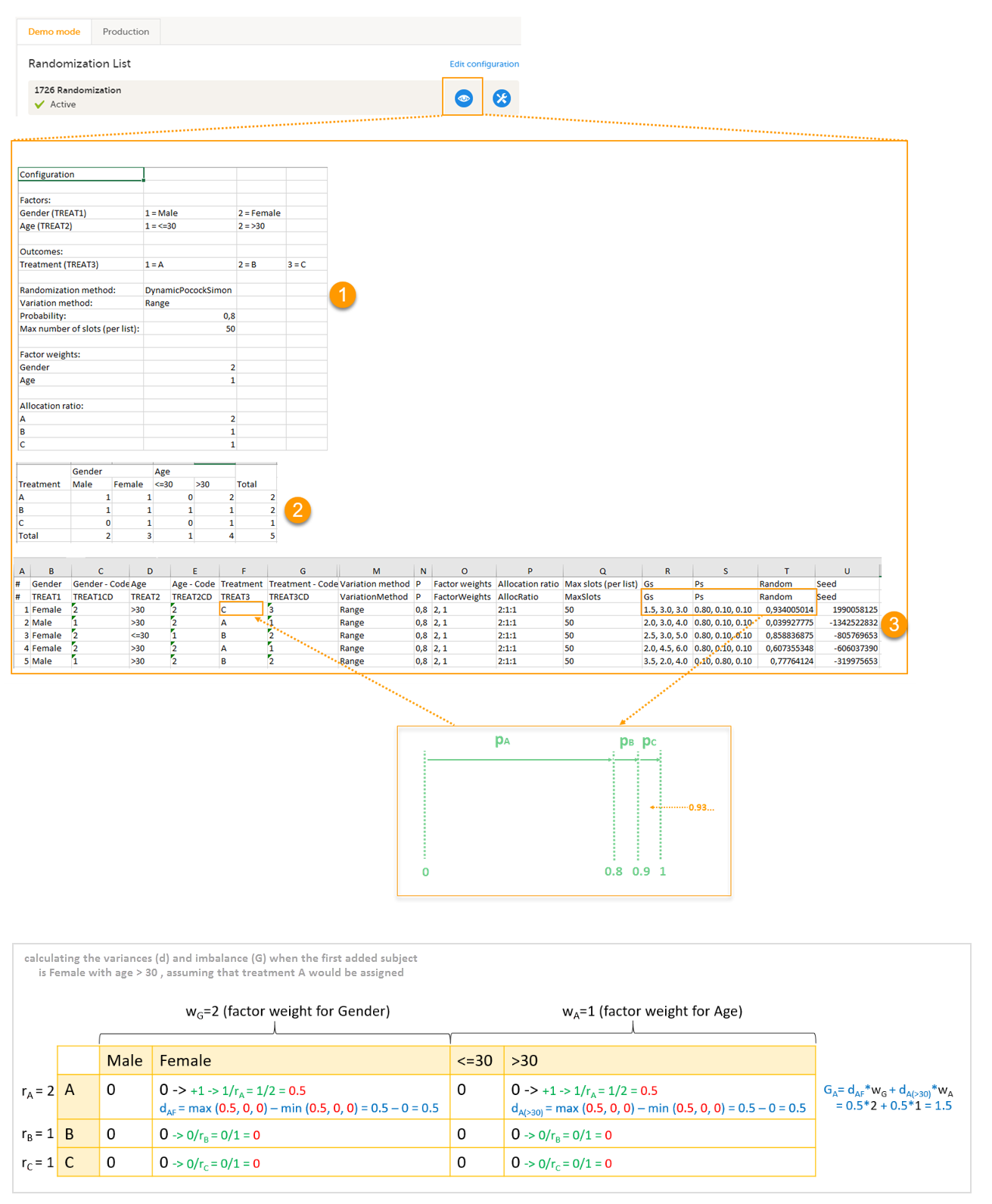
Let's consider the first added subject and take a look at how the first set of calculations is performed in order to assign a randomized treatment.
All the values in the distribution table (illustrated by 2 in the image) are equal to 0 at start point. We are adding a first subject with Gender = Female and Age > 30. For this, we follow the workflow for calculating D, G and P for each of the three possible outcomes (treatments).
We are going to use the following notations:
- Factor weights
- wG - factor weight for gender = 2
- wA - factor weight for age = 1
- Allocation ratios
- rA - allocation ratio for treatment A = 2
- rB - allocation ratio for treatment B = 1
- rC - allocation ratio for treatment C = 1
- Variance
- dAM - variance for treatment = A, and gender = male
- dAF - variance for treatment = A, and gender = female
- dA(<=30) - variance for treatment = A, and age <= 30
- dA(>30) - variance for treatment = A, and age > 30
- dBM, dBF, dB(<=30), dB(>30), dCM, dCF, dC(<=30), dC(>30) - variances for treatment B, respective C, in the same manner as described above for treatment A.
We start by hypothetically assigning each of the three treatments and calculating the variances for each assignment. Because the subject to be added is a female with age > 30, we only have to calculate the variances for those factor values.
- Assuming that treatment A would be assigned, we add 1 to the distribution table, in the row for Treatment A, in the Female column and in the Age > 30 column. The variances for each factor are calculated as below and illustrated by the last table in the image:
- dAF = 1/ rA - 0 = 1/2 = 0.5 (one female subject was added, which makes the highest value in the distribution table corresponding to the Female column = 1 and the lowest = 0)
- dA(>30) = 1/ rA - 0 = 1/2 = 0.5 (one subject was added with age > 30, which makes the highest value in the distribution table corresponding to the Age > 30 column = 1 and the lowest = 0)
- Assuming that treatment B would be assigned, we add 1 to the distribution table, in the row for Treatment B, in the Female column and in the Age > 30 column. The variances for each factor:
- dBF = 1/ rB - 0 = 1 (one female subject was added, which makes the highest value in the distribution table corresponding to the Female column = 1 and the lowest = 0)
- dB(>30) = 1/ rB - 0 = 1 (one subject was added with age > 30, which makes the highest value in the distribution table corresponding to the Age > 30 column = 1 and the lowest = 0)
- Assuming that treatment C would be assigned, we add 1 to the distribution table, in the row for Treatment C, in the Female column and in the Age > 30 column. The variances for each factor:
- dCF = 1/ rC - 0 = 1 (one female subject was added, which makes the highest value in the distribution table corresponding to the Female column = 1 and the lowest = 0)
- dC(>30) = 1/ rC - 0 = 1 (one subject was added with age > 30, which makes the highest value in the distribution table corresponding to the Age > 30 column = 1 and the lowest = 0)
Then we calculate the total amount of imbalance for each of the three possible treatment assignments. These are the values displayed in the table in the Slots sheet (3 in the image), for the first entry, in the Gs column:
- GA = dAFwG + dA(>30)wA = 0.5*2 + 0.5*1 = 1.5
- GB = dBFwG + dB(>30)wA = 1*2 + 1*1 = 3
- GC = dCFwG + dC(>30)wA = 1*2 + 1*1 = 3
Then we calculate the probability (P) for each of the three possible treatment assignments. We have set the probability (p) to 0.8 in our example. The treatment with the lowest G (in our case A) will receive the Probability (P) as p (in our case 0.8). The remaining treamment assignments will split the remaining probability. These are the values displayed in the table in the Slots sheet (3 in the image), for the first entry, in the Ps column:
- PA = 0.8 (thus covering all values greater than or equal to 0 and less than 0.8)
- PB = 0.1 (thus covering all values greater than or equal to 0.8 and less than 0.9)
- PC = 0.1 (thus covering all values greater than or equal to 0.9 and less than 1)
Then we generate a random number between 0 and 1 using Donald E. Knuth's subtractive random number generator algorithm and a seed value based on the number of ticks to represent the current date. The number is displayed in the table in the Slots sheet (3 in the image), for the first entry, in the Random column, in our example Random = 0.934...Considering the probabilities for each treatment assignment, and the random number, treatment C will be assigned to the first subject, as illustrated in the image.
